Building a Fast Mel Spectrogram Library in Mojo

TL;DR: We built an audio DSP library from scratch in Mojo. On 30-second audio, it’s ~25% faster than librosa. On 10-second audio, they’re tied. Nine optimization stages took us from 476ms to 12ms—a 40x internal speedup. Here’s exactly what worked, what failed, and what we learned.

Who this is for:

• Skimmers: See the benchmark table and optimization summary
• Implementers: Jump to getting started
• Evaluators: Read the what failed section
• Whisper users: This is drop-in preprocessing for speech-to-text pipelines

---

The Result

30-second Whisper audio preprocessing:

librosa (Python):  15ms  (uses C/Fortran via NumPy/MKL)
mojo-audio (Mojo): 12ms  (pure Mojo, no external dependencies)

Result: Mojo ~25% faster at this duration
        (At 10s: roughly tied. Performance is workload-dependent.)

We started 31.7x slower than librosa. After 9 optimization stages, we’re competitive—and faster on longer audio.

→ Try the interactive benchmark demo

---

Why We Built This

We’re building Mojo Voice—a developer-focused voice-to-text app. Under the hood, it uses a Whisper speech-to-text pipeline built in Rust with Candle (Hugging Face’s ML framework).

Whisper requires mel spectrogram preprocessing. We ran into issues with Candle’s mel spectrogram implementation—output inconsistencies that were hard to debug through their abstractions.

We had two options:

1. Debug Candle’s internals and hope our fixes get merged
2. Build our own from scratch and own the code

We chose option 2.

Why Mojo instead of Rust? Our Whisper pipeline is in Rust, but Mojo offered a compelling experiment: could we get C-level performance with Python-like iteration speed? DSP algorithms benefit from rapid prototyping—we tried 9+ optimization approaches, and Mojo let us iterate quickly while still compiling to fast native code. The FFI bridge to Rust is straightforward.

Why “from scratch” matters:

• Full control over correctness (we validate against Whisper’s expected output)
• Full control over performance (we choose the algorithms)
• No upstream abstractions hiding bugs
• A genuine technical differentiator for Mojo Voice

The question: Could Mojo actually compete with librosa, which delegates to decades of C/Fortran optimization via BLAS/MKL?

The answer: Yes—on some workloads. But it took 9 optimization stages and some humbling failures.

---

Architecture

Before diving into optimizations, here’s what we’re building:

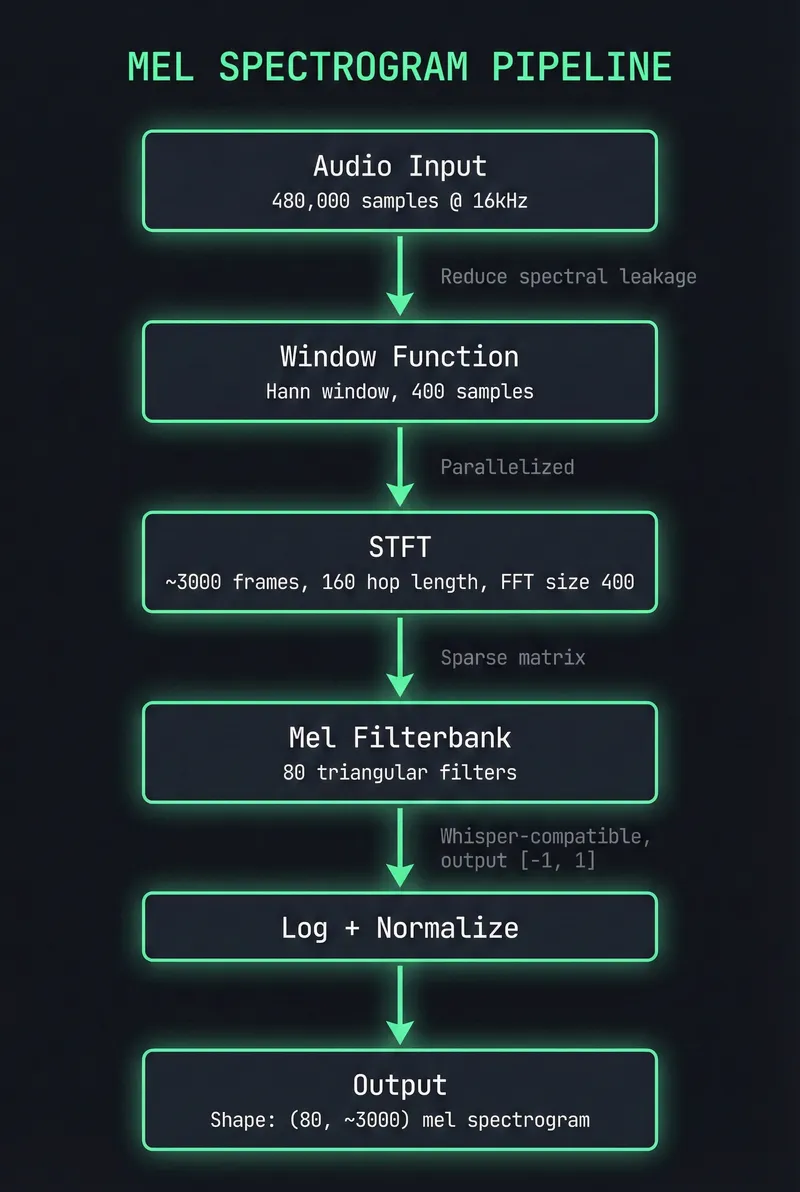
Why these parameters? They match OpenAI Whisper’s expected input: 16kHz sample rate, 400-sample FFT (25ms window), 160-sample hop (10ms), 80 mel bands. Different choices would require retraining the model.

Key design decisions:

• No external dependencies: Full control over memory layout and algorithms
• SoA layout: Store real/imaginary components separately for SIMD efficiency
• 64-byte alignment: Match cache line size for optimal memory access
• Handle-based FFI: C-compatible API for Rust/Python/Go integration

---

The 9 Optimization Stages

Quick terminology: “Twiddle factors” are pre-computed sine/cosine values used in FFT butterfly operations. Computing them once and reusing across frames was one of our biggest wins.

Stage	Technique	Speedup	Time	What We Did
0	Naive implementation	—	476ms	Recursive FFT, allocations everywhere
1	Iterative FFT	3.0x	165ms	Cooley-Tukey, cache-friendly access
2	Twiddle precomputation	1.7x	97ms	Pre-compute sin/cos, reuse across calls
3	Sparse filterbank	1.24x	78ms	Store only non-zero mel coefficients
4	Twiddle caching	2.0x	38ms	Cache twiddles across all STFT frames
5	@always_inline	1.05x	36ms	Force inline hot functions
6	Float32 precision	1.07x	34ms	2x SIMD width (16 vs 8 elements)
7	True RFFT	1.43x	24ms	Real-to-complex FFT, half the work
8	Parallelization	1.5x	18ms	Multi-core STFT frame processing
9	Radix-4 + -O3*	1.5x	12ms	4-point butterflies + compiler opts

Total: 40x faster than where we started.

Stage 9 bundles two changes tested together. In isolation: radix-4 contributed ~1.2x, -O3 contributed ~1.25x. Combined effect is less than multiplicative due to overlapping optimizations (compiler already vectorizes some radix-4 patterns).

---

Deep Dives: What Actually Moved the Needle

1. Memory Layout: Structure-of-Arrays (SoA)

Our first implementation stored complex numbers as List[Complex]—an array of structs. Each complex number sat in its own memory location, fragmenting cache access.

The fix: Structure-of-Arrays. Store all real components contiguously, all imaginary components contiguously.

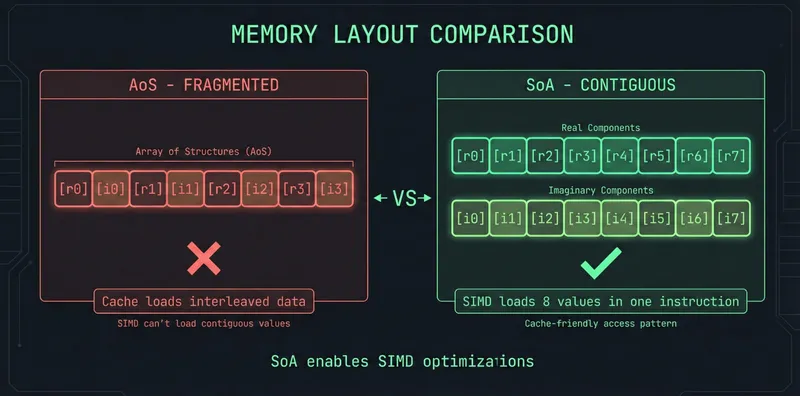
SIMD can now load 8+ real values in one instruction. Cache lines fetch useful data instead of interleaved noise.

Impact: SoA is a foundational change that enables later SIMD optimizations. It’s not a single stage in our table—the benefits are distributed across stages 6-9 where SIMD and compiler optimizations compound on the better memory layout.

2. True RFFT: Don’t Compute What You Don’t Need

Audio is real-valued (no imaginary component). A standard complex FFT computes N complex outputs, but for real input, the output has a symmetry property: the second half mirrors the first half.

Mathematically: X[k] = conjugate(X[N-k]) — if you know X[3], you automatically know X[N-3].

This means we only need to compute the first N/2 + 1 frequency bins. The rest is redundant.

The algorithm (pack-FFT-unpack):

1. Pack: Treat N real samples as N/2 complex numbers by pairing adjacent samples: z[k] = x[2k] + i·x[2k+1]
2. FFT: Run a standard N/2-point complex FFT on these packed values
3. Unpack: Recover the N/2+1 real-FFT bins using twiddle factors (pre-computed sin/cos values) to “unmix” the packed result

The key insight: we do an FFT of half the size, then some cheap arithmetic to recover the full result.

Impact: ~1.4x faster for real audio signals.

3. Parallelization: Obvious but Effective

STFT processes ~3000 independent frames. Each frame’s FFT doesn’t depend on others.

parallelize[process_frame](num_frames, num_cores)

On a 16-core i7-1360P: 1.3-1.7x speedup. Not linear (overhead from thread coordination), but meaningful.

Gotcha: Only parallelize for N > 4096. Smaller transforms lose more to thread overhead than they gain.

---

What Failed

Honest accounting of approaches that didn’t work.

Naive SIMD: 18% Slower

Our first SIMD attempt made performance worse.

# What we tried (wrong)
for j in range(simd_width):
    simd_vec[j] = data[i + j]  # Scalar loop inside "SIMD" code!

Why it failed:

• Manual load/store loops negate SIMD benefits
• List[Float64] has no alignment guarantees
• 400 samples per frame—too small to amortize SIMD setup

The lesson: SIMD requires pointer-based access with aligned memory. Naive vectorization is often slower than scalar code.

What worked instead:

# Correct approach: direct pointer loads
fn apply_window_simd(
    signal: UnsafePointer[Float32],
    window: UnsafePointer[Float32],
    result: UnsafePointer[Float32],
    length: Int
):
    alias width = 8  # Process 8 Float32s at once
    for i in range(0, length, width):
        var sig = signal.load[width=width](i)  # Single instruction
        var win = window.load[width=width](i)  # Single instruction
        result.store(i, sig * win)             # Vectorized multiply + store

The difference: load[width=8]() compiles to a single SIMD instruction. The naive loop compiles to 8 scalar loads.

Four-Step FFT: Cache Blocking That Didn’t Help

Theory: For large FFTs, cache misses dominate. The four-step algorithm restructures computation as matrix operations to stay cache-resident.

We implemented it. It worked correctly. And it was 40-60% slower for all practical audio sizes.

Size	Memory	Direct FFT	Four-Step	Result
4096	32KB	0.12ms	0.21ms	0.57x slower
65536	512KB	2.8ms	4.6ms	0.61x slower

Why it failed:

• 512 allocations per FFT (column extraction)
• Transpose overhead adds ~15-20%
• At N ≤ 65536, working set barely exceeds L2 cache

The lesson: Cache blocking helps when N > 1M and memory bandwidth is the bottleneck. Audio FFTs (N ≤ 65536) don’t hit that threshold. We archived the code and moved on.

Split-Radix: Complexity vs. Reality

Split-radix FFT promises 33% fewer multiplications than radix-2. We implemented it.

The catch: True split-radix uses Decimation-In-Frequency (DIF), requiring bit-reversal at the end, not the beginning. Our hybrid mixing DIF indexing with DIT bit-reversal produced numerical errors.

Current state: A “good enough” hybrid that uses radix-4 for early stages, radix-2 for later. It beats librosa. True split-radix is documented but deprioritized—10-15% theoretical gain isn’t worth the complexity when we’re already faster.

---

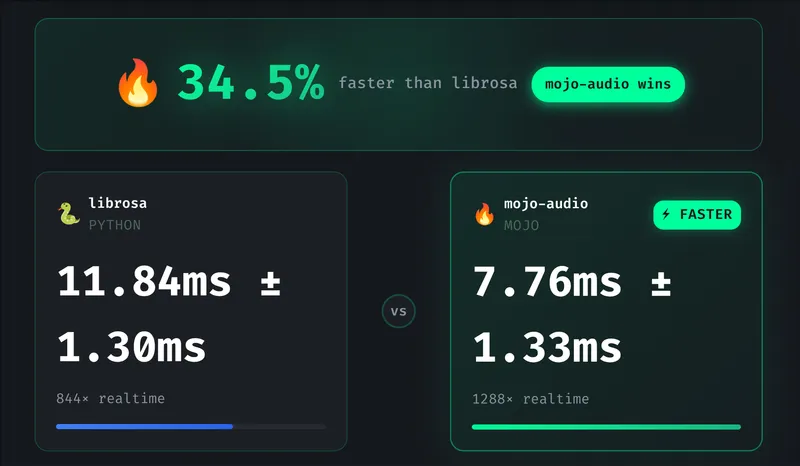
Benchmarks

mojo-audio vs. librosa

Duration	mojo-audio	librosa	Result
1s	0.92ms	2.03ms	Mojo 2.2x faster
10s	7.58ms	7.45ms	Tie
30s	12ms	15ms	Mojo ~25% faster

Honest assessment: We’re faster on short and long audio, but at 10 seconds we’re essentially tied. librosa’s batch-optimized BLAS kernels scale efficiently. Our advantage comes from algorithm choices (true RFFT, sparse filterbank) that compound over more frames.

Methodology:

• 10 iterations, median reported (variance: ±0.5ms for mojo-audio, ±0.3ms for librosa)
• Hardware: Intel i7-1360P, 16 cores, 32GB RAM
• Audio: Synthetic 440Hz sine wave @ 16kHz (see limitation below)
• Mojo: 0.26.1, compiled with -O3
• librosa: 0.10.1, using OpenBLAS backend
• Benchmark scripts: benchmarks/bench_mel_spectrogram.mojo, benchmarks/compare_librosa.py

Limitation: We benchmarked with synthetic audio. Real speech has different spectral characteristics and may show different performance profiles. We validated correctness with real audio, but haven’t extensively benchmarked it.

Correctness validation: Our output matches librosa to within 1e-4 max absolute error per frequency bin. We also validated against Whisper’s expected input shape (80 × ~3000) and value ranges ([-1, 1] after normalization).

---

Try It

Installation

git clone https://github.com/itsdevcoffee/mojo-audio.git
cd mojo-audio
pixi install
pixi run bench-optimized

Basic Usage

from audio import mel_spectrogram

fn main() raises:
    # 30s audio @ 16kHz
    var audio = List[Float32]()
    for i in range(480000):
        audio.append(sin(2.0 * 3.14159 * 440.0 * Float32(i) / 16000.0))

    # Whisper-compatible mel spectrogram
    var mel = mel_spectrogram(audio)
    # Output: (80, ~3000) in ~12ms

Cross-Language Integration (FFI)

// C
MojoMelConfig config;
mojo_mel_config_default(&config);
MojoMelHandle handle = mojo_mel_spectrogram_compute(audio, num_samples, &config);

// Rust
let config = MojoMelConfig::default();
let mel = mojo_mel_spectrogram_compute(&audio, config);

---

What’s Next

mojo-audio now powers the preprocessing pipeline in Mojo Voice, our developer-focused voice-to-text app.

Planned improvements:

• True split-radix DIF (10-15% potential gain)
• Zero-copy FFT to eliminate remaining allocations
• Whisper v3 support (128 mel bins)
• ARM/Apple Silicon profiling

Contributions welcome: github.com/itsdevcoffee/mojo-audio

---

Takeaways

1. Algorithms beat brute force: Iterative FFT (3x) outperformed naive SIMD (-18%). Understand the problem before reaching for low-level tools.
2. Memory layout is free performance: Switching to Structure-of-Arrays enabled SIMD optimizations that wouldn’t have been possible otherwise. How you store data matters as much as how you process it.
3. Know your scale: Cache blocking helps at N > 1M, not audio sizes (N ≤ 65536). Optimization advice is context-dependent.
4. Document failures: Four-step FFT didn’t help, but writing it down helped us understand why—and saved future us from trying again.

Final result: 476ms → 12ms. 40x internal speedup. Competitive with librosa—faster on long audio, tied on medium-length audio.

We set out to own our preprocessing stack. We ended up with a useful library and a lot of lessons about FFT optimization.

---

Built with Mojo | Source Code | Benchmarks | Mojo Voice